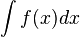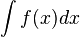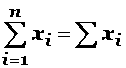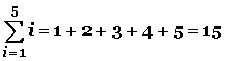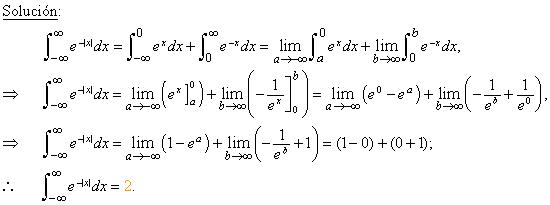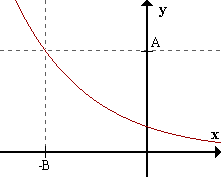INTEGRAL INDEFINIDA Y MÉTODOS DE INTEGRACION

INTEGRAL INDEFINIDA.

En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.

Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.

Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:

EJEMPLOS:

INTEGRALES DIRECTAS.



INTEGRACION CON EXPRECIONES EXPONENCIALES



INTEGRACION DIRECTA DE UNA SUMA



INTEGRACION DIRECTA DE UNA DIVICION



INTEGRACION POR SUSTITUCION O CAMBIO DE VARIABLE






INTEGRALES TRIGONOMÉTRICAS

FORMULAS DE LAS INTEGRALES TRIGONOMÉTRICAS









INTEGRACION POR PARTES






INTEGRACION POR SUSTITUCION TRIGONOMETRICA



EJEMPLO 2:




INTEGRACION POR FRACCIONES PARCIALES

Read More

TEOREMA FUNDAMENTAL DEL CALCULO

Medición aproximadas de figuras amorfas 

La Aproximada de Figuras Amorfas

Calcular las áreas de una figura regular es una tarea muy fácil, por lo cual la sustitución de la longitud, anchura u otras cantidades en la fórmula produciría el resultado.

Sin embargo, la estimación del área bajo la curva de las funciones no es tan sencilla ya que existen figuras amorfas y no fórmulas directas para estima resta área.

integración puede ser utilizada fructífera mente en una situación semejante.

Existen cuatro gráficas posibles para las cuales el área necesita ser evaluada.

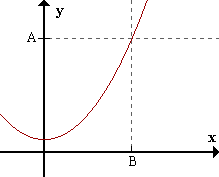
Estas son: 1 Cuando el área está limitada por la curva y = f(x), el eje x y las ordenadas x = a y x = b.

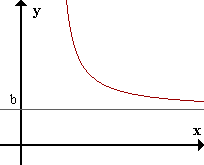
El gráfico de la función se muestra a continuación.

Para estimar el área de tal figura, considere el área bajo la curva está compuesto por un gran número de delgadas tiras verticales.Suponiendo que hay una tira arbitraria y para la altura y una dx para la anchura. El área de esta tira elemental sería, dA = y dx donde y = f(x)

El área total A de la región entre el eje x, la ordenada x = a y x = b y la curva y = f (x) será la sumatoria de las áreas de todas las tiras elementales en toda la región o la zona limitada.

reduce la fórmula, A = dA = y dx = f(x) dx La integral anterior puede ser evaluada mediante poner la función en su lugar e integrándola.

2 La segunda situación es cuando el área está delimitada por la curva x = g(y), el eje y, y las ordenadas y = y1 y y2 = y. La gráfica de la función se muestra a continuación.

Asuma que el área bajo la curva está compuesta de un gran número de tiras delgadas horizontales. Sea una tira arbitraria dypara la altura y xpara la longitud. El área de esta tira elemental sería, dA = x dy donde x = g(y)

El área total A de la región entre el eje x, la ordenada y = y1 y y2 = y, y la curva x = g(y) será la sumatoria de las áreas de todas las tiras elementales en toda la región o el área limitada. Esto produce la fórmula, 

A = dA = x dy = g(y) dy

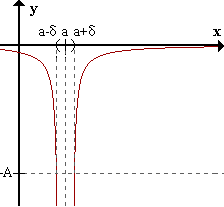
3 Se presenta una tercera situación cuando la curva en cuestión se encuentra por debajo del eje x, entonces f(x) es menor que cero desde x = a hasta x = b, el área limitada por la curva y = f(x) y las ordenadas x = a y x = b, y el eje x es negativo.

Pero el valor numérico del área debe ser tomado en consideración ,entonces

A = | f(x) dx|

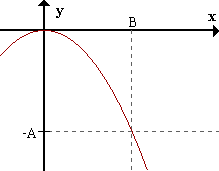
4 Una última posibilidad sería que una parte de la curva esté por encima del eje x y otra parte esté por debajo del eje x. Sea A1 el área debajo del eje x y A2 el área por encimadel eje x. Por lo tanto, el área limitada por la curva y = f(x), el eje x y las ordenadas x = a y x = b serán,

A = |A1| + A2

Tomemos ahora un ejemplo para entender la solución de tales problemas,

Encuentre el área de la región limitada por la curva y2 = x y las rectas x = 1, x = 4 y por el eje x

La curva y2 = x es una parábola con su vértice en el origen. El eje de x es la línea de simetría la cual es el eje de la parábola. El gráfico de la función dada sería,

El área de la región limitada es,

A = y dx = dx = 2/3 [x3/2]14 = 2/3 [43/2 – 13/2] = 2/3 [8 – 1] = 14/3

NOTACIÓN SUMATORIA

La sumatoria o sumatorio es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumados.

La operación sumatoria se expresa con la letra griega sigma mayúscula Σ,  y se representa así:

Expresión que se lee: "sumatoria de Xi,  donde i toma los valores desde 1 hasta n".

i es el valor inicial, llamado límite inferior.

n es el valor final, llamado límite superior.

Pero necesariamente debe cumplirse que:

i ≤ n

Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:

Ahora, veamos un ejemplo:
Si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:

SUMA DE RIEMAN

 Las sumas de Riemann son un método para aproximar el área total bajo la gráfica de una curva. Llevadas al límite se obtiene la integral de Riemann.

EJEMPLO 2:

EJEMPLO 3:




LA INTEGRAL DEFINIDA

La integral definida se representa por símbolo integral definida.

∫ es el signo de integración.

a límite inferior de la integración.

b límite superior de la integración.

f(x) es el integrando o función a integrar.

(dx) es diferencial de x, e indica cuál es la variable de la función que se integra.

Propiedades de la integral definida

1. El valor de la integral definida cambia de signo si se permutan los límites de integración.

2. Si los límites que integración coinciden, la integral definida vale cero.

3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].

4. La integral definida de una suma de funciones es igual a la suma de integrales.

5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

TEOREMA FUNDAMENTAL DEL CALCULO

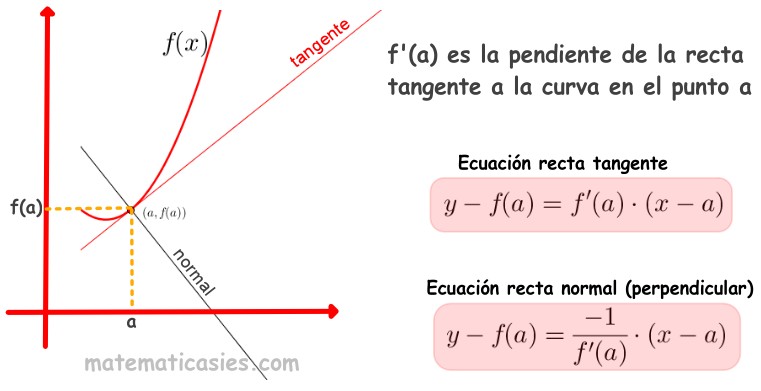
Teorema fundamental del cálculo F'(x) = f(x) El teorema fundamental del cálculo nos indica que la derivación y la integración son operaciones inversas. Al integrar una función continua y luego derivarla se recupera la función original.



EJEMPLO 2




VALOR MEDIO PARA INTEGRALES


Si una función es continua en un intervalo cerrado [a, b], existe un punto c en el interior del intervalo tal que

EJEMPLO 2:

EJEMPLO 3:





EJEMPLO 4:





EJEMPLO 5:





EJEMPLO 6:





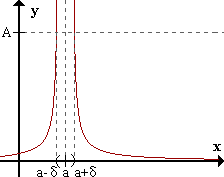
INTEGRALES IMPROPIAS

Llamaremos integral impropia de primera especie aquella cuyo intervalo de integración es infinito, ya sea de la forma (a,∞), (−∞, b) o bien (−∞,∞),

EJERCICIOS:

Read More

APLICACIONES DE LAS DERIVADAS

RECTA TANGENTE Y RECTA NORMAL A UNA CURVA EN EL PUNTO DADO.

Recta tangente

Desde la escuela primaria se sabe que la recta tangente en un punto de una circunferencia es aquella recta que intercepta a la circunferencia en un solo punto, pero lo cierto es que tal definición no es suficiente para una curva en general porque en otros casos la recta tangente puede llegar a interceptar a la curva en uno o más puntos, además de ser inclinada, horizontal o vertical.

TEOREMA DE ROLLE

El teorema de Rolle dice que:

Si f es una función continua en [a, b] y derivable en (a, b), tal que f(a) = f(b), hay algún punto c pertenece (a, b) en el que f'(c) = 0

La interpretación gráfica del teorema de Rolle nos dice que hay un punto en el que la tangente es paralela al eje de abscisas.

TEOREMA DE LAGRANGE O TEOREMA DEL VALOR MEDIO DEL CALCULO DIFERENCIAL.

Teorema del valor medio

El teorema del valor medio o de Lagrange dice que:

Sea f es una función continua en [a, b] y derivable en (a, b), existe un punto c pertenece (a, b) tal que:

FUNCIÓN CRECIENTE 

Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x1  y x2, con la condición x1 £ x2, se verifica que f( x1 ) < f( x2 ).

Se dice estrictamente creciente si de x1 < x2 se deduce que f(x1) < f(x2).

Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x1  y x2, que cumplan x1 £ x2, entonces f(x1 ) ³ f(x2 ).

Siempre que de x1 < x2 se deduzca f(x1 ) > f(x2 ), la función se dice estrictamente decreciente.

Read More

DERIVADAS

Derivada.
La derivada de una función en un punto es la pendiente de la recta tangente a la función en dicho punto.

Formulas de Derivación.



Interpretación Geométrica de la Derivada.

PENDIENTE DE UNA RECTA.

FORMULA GENERAL PARA ENCONTRAR LA ECUACIÓN DE LA RECTA TANGENTE.

y-y1 = m (x-x1)

PROPIEDADES DE LAS DERIVADAS

Las derivadas forman una parte importante del cálculo. Hablando en términos sencillos, la derivada es una medida de la tasa de variación de la salida de una función así como varía la entrada de la función. En base a la definición anterior está claro que la salida de la función es una función de la entrada de la función. Las derivadas tienen algunas propiedades especiales que son importantes estudiar antes de saltar de lleno en el tema.

Derivadas (ejercicios).

DERIVADA DE UNA CONSTANTE.





DERIVADA DE UNA CONSTANTE POR UNA VARIABLE.

DERIVADAS DE FUNCIONES ALGEBRAICAS.

DERIVADAS EXPONENCIALES.





REGLA DE LA CADENA.









DERIVADA DE FUNCIONES TRIGONOMETRICAS.









REGLAS PARA DERIVACIONES LOTGARIMICAS.

Read More

LIMITES Y CONTINUIDADES

Limite.

Línea real o imaginaria que marca el fin de una superficie o cuerpo o la separación entre dos entidades.

Limite de una función.



Limite trigonométrico.

Limite de una sucesión.

El límite de una sucesión es uno de los conceptos más antiguos del análisis matemático. El mismo da una definición rigurosa a la idea de una sucesión que se va aproximando hacia un punto llamado límite. Si una sucesión tiene límite, se dice que es una sucesión convergente, y que la sucesión converge o tiende al límite. En caso contrario, la sucesión es divergente.

Limites infinitos

Caso 1:

lim_x->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) > A.

El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.

Caso 2:

lim_x->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) < -A.

Caso 3:

lim_x->+inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) > A.

Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.

Caso 4

lim_x->+inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) < -A.

Caso 5:

lim_x->-inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) > A.

Caso 6:

lim_x->-inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) < -A.

Caso 7:

lim_x->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todo x > Bf(x) pertenece al E_b,ε.

Caso 8:

lim_x->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todo x < -Bf(x) pertenece al E_b,ε.

limites infinitos(ejercisios).

ejercicio 2.

ejercicio 3.

Ejercicio 4.

Asintotas.

Se llama asíntota de una función f(x) a una recta t cuya distancia a la curva tiende a cero, cuando x tiende a infinito o bien x tiende a un punto a.

Asíntota vertical

La recta x=a es asíntota vertical (AV) de f(x) si lim_x->a+ f(x) = inf olim_x->a- f(x) = inf.

Asíntota horizontal

La recta y=b es asíntota horizontal (AH) de f(x) si lim_x->inf f(x) = b

Ejercicios.





Tipos de Asinsotas.





Asintotas mediante limites.

Read More

RECTA NUMERICA

 RECTA NUMÉRICA.

 La recta numérica está compuesta de números enteros positivos, números enteros negativos y el cero. El cero se llama el origen.

 
ECUACIONES Y DESIGUALDADES.
a) Ecuaciones: cuando se cumple la igualdad solamente para determinado(s) valor(es) de
la(s) variable(s).

Ejemplo: 
3x-7 = 5 
3x=5+7
x=12/3
x=4 , se cumple que es igual solamente cuando x = 4.
ejemplo 2:   
2x+10=20
2x=20-10
x=10/2
x=5

ejemplo 3:
2x=6
x=6/2
x=3

ejemplo 4:
2x-3=6+x
2x-x=6+3
x=9

Desigualdades.
Solución de una desigualdad lineal:



Solucion de una ecuación cuadratica.

valor absoluto

 En matemática, el valor absoluto o módulo de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo o negativo. Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.

Ejemplo 1. | x − 4| = 3

Solución: Hay dos posibilidades

x-4 =3 o x-4=-3.

ejemplo 2:

|5-4x|= 3

soluciones únicas

5-4x = 3 y 5-4x= -3

Read More