APLICACIONES DE LAS DERIVADAS

RECTA TANGENTE Y RECTA NORMAL A UNA CURVA EN EL PUNTO DADO.

Recta tangente

Desde la escuela primaria se sabe que la recta tangente en un punto de una circunferencia es aquella recta que intercepta a la circunferencia en un solo punto, pero lo cierto es que tal definición no es suficiente para una curva en general porque en otros casos la recta tangente puede llegar a interceptar a la curva en uno o más puntos, además de ser inclinada, horizontal o vertical.

TEOREMA DE ROLLE

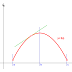
El teorema de Rolle dice que:

Si f es una función continua en [a, b] y derivable en (a, b), tal que f(a) = f(b), hay algún punto c pertenece (a, b) en el que f'(c) = 0

La interpretación gráfica del teorema de Rolle nos dice que hay un punto en el que la tangente es paralela al eje de abscisas.

TEOREMA DE LAGRANGE O TEOREMA DEL VALOR MEDIO DEL CALCULO DIFERENCIAL.

Teorema del valor medio

El teorema del valor medio o de Lagrange dice que:

Sea f es una función continua en [a, b] y derivable en (a, b), existe un punto c pertenece (a, b) tal que:

FUNCIÓN CRECIENTE 

Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x1  y x2, con la condición x1 £ x2, se verifica que f( x1 ) < f( x2 ).

Se dice estrictamente creciente si de x1 < x2 se deduce que f(x1) < f(x2).

Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x1  y x2, que cumplan x1 £ x2, entonces f(x1 ) ³ f(x2 ).

Siempre que de x1 < x2 se deduzca f(x1 ) > f(x2 ), la función se dice estrictamente decreciente.