La derivada de una función en un punto es la pendiente de la recta tangente a la función en dicho punto.
Formulas de Derivación.

Interpretación Geométrica de la Derivada.
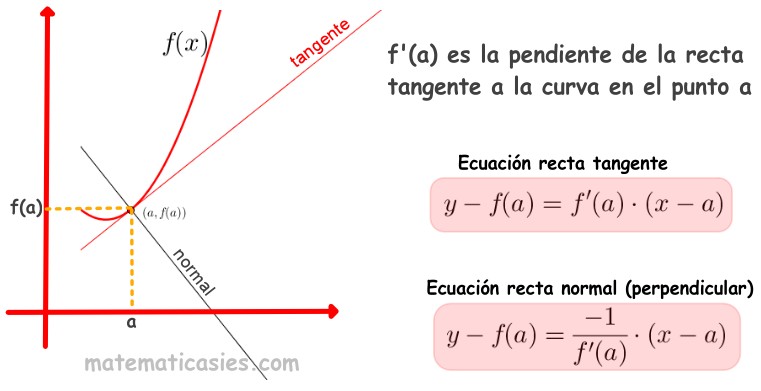
PENDIENTE DE UNA RECTA.
FORMULA GENERAL PARA ENCONTRAR LA ECUACIÓN DE LA RECTA TANGENTE.
y-y1 = m (x-x1)
PROPIEDADES
DE LAS DERIVADAS
Las
derivadas forman una parte importante del cálculo. Hablando en términos
sencillos, la derivada es una medida de la tasa de variación de la salida de
una función así como varía la entrada de la función. En base a la definición
anterior está claro que la salida de la función es una función de la entrada de
la función. Las derivadas tienen algunas propiedades especiales que son
importantes estudiar antes de saltar de lleno en el tema.
Derivadas (ejercicios).
DERIVADA DE UNA CONSTANTE.
DERIVADA DE UNA CONSTANTE POR UNA VARIABLE.
DERIVADAS DE FUNCIONES ALGEBRAICAS.
DERIVADAS EXPONENCIALES.
REGLA DE LA CADENA.
DERIVADA DE FUNCIONES TRIGONOMETRICAS.
REGLAS PARA DERIVACIONES LOTGARIMICAS.










0 comentarios:
Publicar un comentario