En cálculo infinitesimal, la
función primitiva o antiderivada de una función f es una función F cuya
derivada es f, es decir, F ′ = f.
Una condición suficiente
para que una función f admita primitivas sobre un intervalo es que sea continua
en dicho intervalo.
Si una función f admite una
primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en
una constante: si F1 y F2 son dos primitivas de f, entonces existe un número
real C, tal que F1 = F2 + C. A C se le conoce como constante de integración.
Como consecuencia, si F es una primitiva de una función f, el conjunto de sus
primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se
representa como:
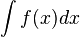
EJEMPLOS:
INTEGRALES DIRECTAS.
INTEGRACION CON EXPRECIONES EXPONENCIALES
INTEGRACION DIRECTA DE UNA SUMA
INTEGRACION DIRECTA DE UNA DIVICION
INTEGRACION POR SUSTITUCION O CAMBIO DE VARIABLE
INTEGRALES TRIGONOMÉTRICAS
FORMULAS DE LAS INTEGRALES TRIGONOMÉTRICAS

INTEGRACION POR PARTES
INTEGRACION POR SUSTITUCION TRIGONOMETRICA
EJEMPLO 2:
INTEGRACION POR FRACCIONES PARCIALES










0 comentarios:
Publicar un comentario