LIMITES Y CONTINUIDADES

Limite.

Línea real o imaginaria que marca el fin de una superficie o cuerpo o la separación entre dos entidades.

Limite de una función.



Limite trigonométrico.

Limite de una sucesión.

El límite de una sucesión es uno de los conceptos más antiguos del análisis matemático. El mismo da una definición rigurosa a la idea de una sucesión que se va aproximando hacia un punto llamado límite. Si una sucesión tiene límite, se dice que es una sucesión convergente, y que la sucesión converge o tiende al límite. En caso contrario, la sucesión es divergente.

Limites infinitos

Caso 1:

lim_x->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) > A.

El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.

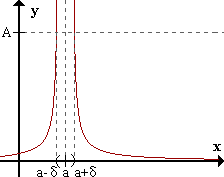
Caso 2:

lim_x->af(x) = -inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E^*_a,δ f(x) < -A.

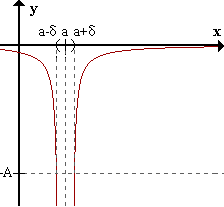
Caso 3:

lim_x->+inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) > A.

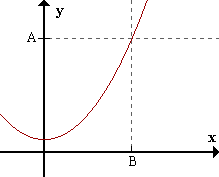
Para cualquier número positivo A (por grande que sea), es posible encontrar un número positivo B tal que para todos los x mayores que B, f(x) es mayor que A. Es decir que f(x) puede ser mayor que cualquier número, si x es lo suficientemente grande.

Caso 4

lim_x->+inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox > B f(x) < -A.

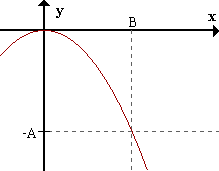
Caso 5:

lim_x->-inff(x) = +inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) > A.

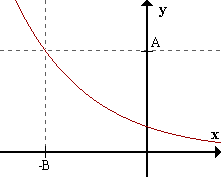
Caso 6:

lim_x->-inff(x) = -inf <=> para todo A > 0 existe B > 0 / para todox < -B f(x) < -A.

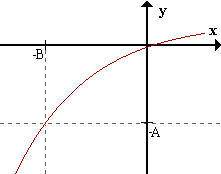
Caso 7:

lim_x->+inff(x) = b <=> para todo ε > 0 existe B > 0 / para todo x > Bf(x) pertenece al E_b,ε.

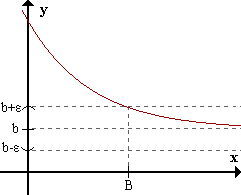
Caso 8:

lim_x->-inff(x) = b <=> para todo ε > 0 existe B > 0 / para todo x < -Bf(x) pertenece al E_b,ε.

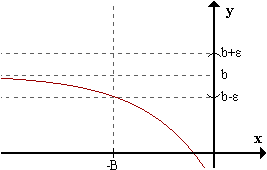
limites infinitos(ejercisios).

ejercicio 2.

ejercicio 3.

Ejercicio 4.

Asintotas.

Se llama asíntota de una función f(x) a una recta t cuya distancia a la curva tiende a cero, cuando x tiende a infinito o bien x tiende a un punto a.

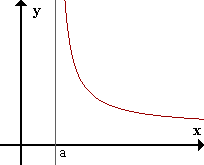
Asíntota vertical

La recta x=a es asíntota vertical (AV) de f(x) si lim_x->a+ f(x) = inf olim_x->a- f(x) = inf.

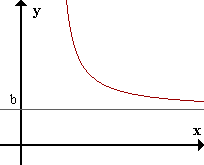
Asíntota horizontal

La recta y=b es asíntota horizontal (AH) de f(x) si lim_x->inf f(x) = b

Ejercicios.





Tipos de Asinsotas.





Asintotas mediante limites.